近日，太阳成集团tyc234cc凝聚态物理与材料物理研究所陈基研究员课题组与字节跳动研究部合作，发展了以神经网络量子蒙特卡洛方法为基础的计算固体体系电极化及原子间受力的高精度第一性原理方法。相关研究成果以“多体神经网络波函数的电极化”（Electric Polarization from a Many-Body Neural Network Ansatz）和“固体神经网络波函数的力与应力计算”（Force and stress calculation with neural network wavefunction for solids）为题，分别在《物理评论快报》（Physical Review Letters）和《法拉第讨论》（Faraday Discussions）发表。

使用第一性原理方法计算材料性质是理解和预测材料的重要手段。目前使用最广泛的第一性原理计算方法是密度泛函理论方法。但就固体的电极化及介电响应计算而言，此前研究表明密度泛函理论的精度并不能令人满意。与密度泛函理论不同，量子蒙特卡洛能够对电子的多体关联给出直接的处理，从而得到精确的基态解。传统的量子蒙特卡洛受限于波函数的拟设形式简单，直接的变分求解无法满足精度需求。采用扩散蒙特卡洛等方法能够进一步提高计算能量的精度，但是在计算介电响应和力等其他物理量时遇到了很大挑战。

团队基于神经网络波函数方法发展了新的固体电极化计算方法，通过神经网络波函数克服了传统拟设的精度困难，从而实现了在变分蒙特卡洛框架下得到固体的电极化性质高精度计算结果。该新计算方法的有效性和准确性在多个体系下得到了验证，例如图1 所展示，在一维氢链和三维碱金属氢化物上，该方法（DeepSolid, DS）能够和量子化学“金标准” CCSD(T) 以及实验结果符合得很好。作为对比，密度泛函理论以及 Hartree-Fock (HF) 方法显著高估了极化率和介电常数。团队也首次对双层石墨烯的面外介电常数进行了精确计算，为实验测量提供了高质量的理论参考。

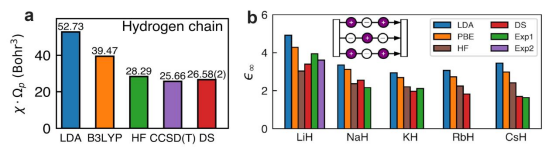
图1(a)不同方法的一维氢链电极化率计算结果(b)不同方法的碱金属氢化物介电常数计算结果。LDA 和 B3LYP 是两种不同的密度泛函；HF 代表 Hartree-Fock 计算方法；CCSD(T) 是一种耦合簇方法，被认为是量子化学“金标准”，但只能做非周期体系再做外推；DS 代表本研究发展的方法。

在固体物理研究中，给定晶体构型的原子间受力以及应力张量计算也是需要计算的基本物理量。力和应力是固体结构优化、声子计算、动力学模拟的重要基础。在传统的量子蒙特卡洛框架下，原子间受力的计算会有很大的统计误差，国际上只有极少的课程组能够实现有效的固体中力和应力的计算。人们在传统的量子蒙特卡洛框架中提出了很多的改进的方案，但是收效甚微。该困难也是量子蒙特卡洛在材料模拟中未能被大规模推广的重要因素之一。在前期的工作中，团队发现应用神经网络波函数和量子蒙特卡洛结合的方法可以有效改进分子中力的计算[Y. Qian,et al. The Journal of Chemical Physics157, 164104 (2022)]。受此启发，团队进一步对在固体中实现力和应力的计算方法进行了研究，提出了一种新的计算原子间受力的方案（fast-warp）。如图 2 所展示的，该方法相比于之前的各种方案，在神经网络变分蒙特卡洛框架中，能够以更高的效率获得更高精度的结果。同时，本研究也发现神经网络的周期性输入特征对某些原子间力计算方案的结果有显著的影响，并提出了一种新的输入特征以提高计算结果的稳健性。本研究也实现并验证了应力张量的计算可行性。高精度的力和应力为未来神经网络蒙特卡洛在材料计算中的进一步应用奠定了基础。

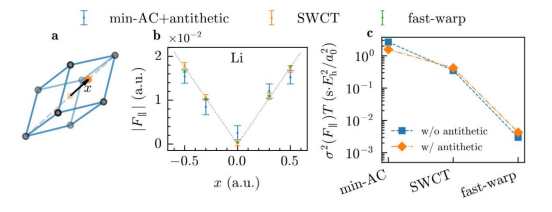
图2(a)氢化锂原胞及氢原子（橙色）位移示意图(b)三种不同计算方案得到的氢原子不同位移时的受力结果。本研究提出的方法（fast-warp）用绿色表示。虚线为能量曲线的拟合结果(c)在石墨烯体系中，不同计算方法单位计算时间的统计误差，越低说明越高效。

太阳成集团tyc234cc2023级博士研究生钱昱冰和字节跳动研究部李向博士是第一篇文章的共同第一作者，李向和陈基是共同通讯作者。钱昱冰是第二篇文章的第一作者，李向是第二作者，陈基是通讯作者。研究工作得到了国家自然科学基金、国家重点研发计划、中国科学院先导专项、太阳成集团tyc234cc轻元素量子材料交叉平台、太阳成集团tyc234cc纳光电子前沿科学中心等的支持。

论文原文链接：

• 【1】https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.176401

• 【2】https://pubs.rsc.org/en/Content/ArticleLanding/2024/FD/D4FD00071D