近日，太阳成集团tyc234cc科维理天文与天体物理研究所教授李立新及其博士生申佳音与中国科学院大学卡弗里理论科学研究所副教授彭程合作，针对将多个时空沿共同交界面粘合的物理结构，发展了一套创新的几何处理技术——书页几何（Booklet Geometry)。这项工作不仅明确了交界处的引力分布，还成功推导出关键的多路径连接条件（Multiway Junction Condition)。该研究有望在黑洞信息悖论领域中做出贡献，为理解黑洞信息丢失问题提供新的视角与理论支持。2024年9月26日，相关成果以“多边界时空的多路径连接条件”（Multiway Junction Conditions for Spacetimes with Multiple Boundaries）为题，在线发表于《物理评论快报》（Physical Review Letters）。

将两个不同的时空沿共同交界面粘合，以获得所需的物理属性，是构建引力理论模型的常用手段。两个时空在粘合处的引力必须是兼容的，因此需要一个匹配条件作为物理约束，称之为连接条件。该问题最早由Darmois和Israel根据前人的工作基础系统地解决，得到了著名的Darmois-Israel连接条件。随着副本虫洞（Replica Wormhole）等技术的出现，多边界几何配置在黑洞信息悖论研究中的重要性日益增长。多个时空沿共同界面的粘合提供了一种不同于副本虫洞的几何结构，同样可能在引力路径积分中发挥作用，因为引力路径积分需要对所有可能的拓扑进行求和。

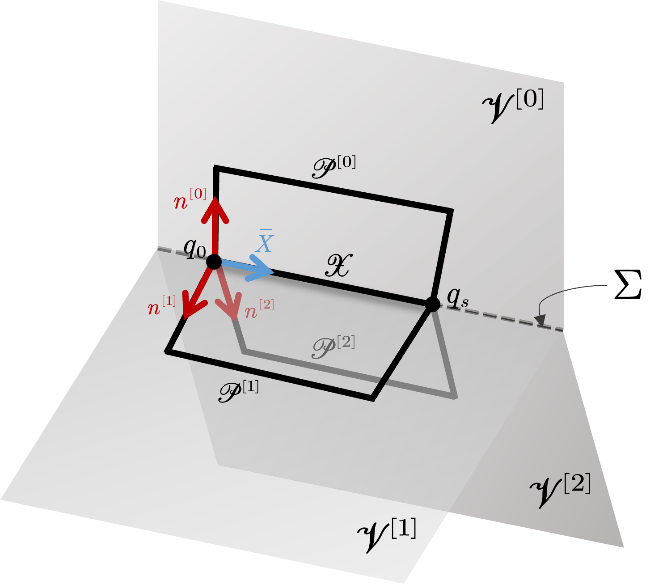
图1. 示例：三书页结构的书册

然而，与经典粘合不同，多时空粘合会改变交界处的微分结构，使得计算交界处的引力变得极为困难。为了解决这一问题，该研究提出并发展了“反向延拓法”，建立了“书页几何”，推导出多路径连接条件。如图所示，在书页几何的形式体系中，每一个被粘合的时空形象地称为一个“书页”，而所有时空粘合而成的整体则称为“书册”。在每个书页中，交界面的嵌入可以用“外曲率”进行描述，且存在唯一的法矢量，指向交界面在该书页中的垂直方向。反向延拓法是将书册嵌入到一个具有足够维度的外部流形中，通过严谨的论证，可以证明所有法矢量之间满足一定的代数关系，称为法矢量的连续性条件。任意选取一个书页，沿法矢量的反方向可以延拓出一个辅助的时空。该辅助时空的引力依赖于所有其他书页，而与选取的书页没有直接关联。因此，选取的书页与该辅助时空的连接可以视为两个不同属性时空的粘合，通过应用经典的Darmois-Israel连接条件，得出了所有书页之间的多路径连接条件。这一结果不依赖于被延拓时空的选择，也不依赖于具体的延拓方式和外部流形的构造，因此多路径连接条件是具有物理意义的内禀约束。在几何与拓扑方面，反向延拓法对时空粘合的前提限制非常宽松，同时具备较强的普适性、严格性和一般性。进一步，该研究又独立地使用作用量变分的方法，得到了完全相同的连接条件，为反向延拓法提供了交叉检验。随后，该研究将多路径连接条件应用于近年来在黑洞信息悖论发展中扮演关键角色的dilaton引力模型和Jackiw-Teitelboim引力模型，取得了一系列重要成果。

图2. 书册几何及反向延拓法的概念展示

太阳成集团tyc234cc天文学系2019级博士生申佳音为论文第一作者，李立新为第二作者，彭程为通讯作者。上述研究工作得到国家自然科学基金和中央高校基本科研专项资金的资助。

论文原文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.131601