2022年11月30日，《科学》（Science）以“新方法解决微积分未解难题，促进高精度粒子物理计算”（Method for solving notorious calculus problems speeds particle physics computations）为题，长篇报道了太阳成集团tyc234cc马滟青研究员课题组在微扰量子场论研究中取得的突破性进展。

文中以下图为例，介绍了微扰量子场论中的基本单元——费曼图和费曼积分。文中强调费曼积分在粒子物理领域的计算中具有不可或缺的地位，不论是对于预言缪子的磁矩，还是对于估量希格斯粒子在大型强子对撞机（LHC）中的产率，无一例外。然而，费曼积分计算是一个极其困难的问题，自从上世纪中叶量子场论兴起以来，它就一直困扰着粒子物理学家。三位在微扰量子场论方面造诣精深的理论物理学家接受了该文采访。马克斯·普朗克物理研究所所长Johannes Henn教授指出，理论计算与LHC实验结果的对比是探索粒子物理标准模型的“破缺”，进而发现新物理效应的必经之路，然而理论上的瓶颈就在于人们计算费曼图和费曼积分的能力不足。匹兹堡大学的Ayres Freitas教授指出，在很多情况下，理论学家甚至连双圈费曼积分的计算都难以完成。

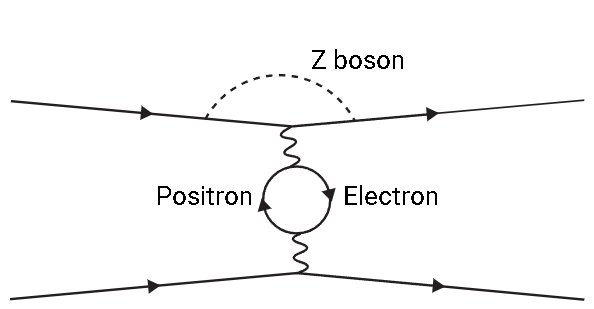
一个正、负电子对之间散射的一个双圈费曼图

2017年，马滟青课题组提出计算费曼积分的辅助质量流方法[Liu X, Ma YQ, Wang CY. Phys. Lett. B, 2018; DOI: 10.1016/j.physletb.2018.02.026]，经过近五年持续、深入的研究，最终把费曼积分计算问题简化为线性代数问题[Liu ZF, Ma YQ. Phys. Rev. Lett, 2022; DOI: 10.1103/PhysRevLett.129.222001]。该文对此方法做了详细介绍。早在上世纪90年代人们就已经知道，利用线性代数可以把给定圈数的任意费曼积分表示为有限个主积分的线性组合，同时，还能够利用线性代数信息建立起这些主积分之间封闭的线性微分方程组。只要给出边界条件，通过非常成熟的数值求解微分方程组的方法，就能够得到所有费曼积分的结果；然而，得到边界条件并非易事。马滟青等人提出，在原始费曼积分中引入辅助质量参数，并指出辅助参数趋于无穷大的时候修改后的费曼积分本质上简化为了“无外腿的真空积分”。一旦有了真空积分的值，通过求解关于辅助参数的微分方程组，就能够实现把辅助参数从无穷大流至零点，即得到了原始的费曼积分。从马滟青课题组的最新进展中可以发现，在辅助质量流框架下计算给定圈数的真空积分，只需要把少一圈的真空积分作为输入；不断地循环利用这一关系，最终除了线性代数信息外只剩下平凡的输入，从而费曼积分计算问题被简化为线性代数问题。由于线性代数问题总是能够系统地求解，所以就得到了计算费曼积分的系统方法。

该文中接受采访的专家对马滟青课题组的新方法给出了高度评价。Ayres Freitas认为，有时候人们对费曼积分提出一些深刻的数学见解，在实际计算中却无济于事，然而马滟青课题组的方法将有助于费曼积分的计算。美因茨大学Stefan Weinzierl教授指出，该方法原则上普适于任何场景，可用以处理任意费曼积分，运用效果好得令人惊讶。

马滟青课题组的刘霄（太阳成集团tyc234cc2021届博士毕业生，目前是英国牛津大学博士后）、王辰宇（太阳成集团tyc234cc2019届博士毕业生，目前是德国卡尔斯鲁厄大学博士后）和刘志峰（太阳成集团tyc234cc2017级在读博士研究生）直接参与了文中所述研究，为取得突破性进展做出重要贡献。

马滟青课题组的上述系列工作得到国家自然科学基金、国家重点研发计划，及核物理与核技术国家重点实验室、太阳成集团tyc234cc高能物理研究中心和太阳成集团tyc234cc高性能计算平台的资助与支持。

专题报道原文链接：

https://www.science.org/content/article/method-solving-notorious-calculus-problems-speeds-particle-physics-computations